Поговоримо про дуже цікаву річ, з якою так чи інакше майже щодня «працює» кожен з нас, проте далеко не кожен це усвідомлює. Поговоримо про рельєф.
Згідно з класичним визначенням, рельєф – це сукупність нерівностей земної поверхні. Тобто рельєф – це лише форма. Однак саме в цьому випадку можна сказати, що для людини ця форма дуже часто стає важливішою за зміст. Уявіть собі дві кулі, металеву та пластмасову. Що в них загального? Вірно, здатність до легкого переміщення у просторі саме через свою форму. Штовхнув – покотилося.
Рельєф також може надавати певні здібності природним та антропогенним об’єктам лише за рахунок їх територіального розміщення. Наприклад, для нашої півкулі північні схили пагорбів або стіни будівель завжди будуть отримувати сонячного тепла більше за інші. Відповідно, на південних схилах будуть утворюватися специфічні біоценози, формуватись відмінні від оточуючих ґрунти. При цьому літологічна будова пагорбу за ландашфтоутворюючим впливом відступатиме на другий план.
Без впливу рельєфу не відбувається жодний природний або антропогенний процес.
Течія води в річці, напрямок вітру, планування забудови міста, перемикання передачі у автівці при підйомі вгору… Ми маємо миритися с рельєфом, вживатися в нього, використовувати його особливості для наших потреб.
Проте щоб щось використовувати, треба про це «щось» знати якомога більше. При цьому ефективність використання буде прямо пропорційна до наших знань.
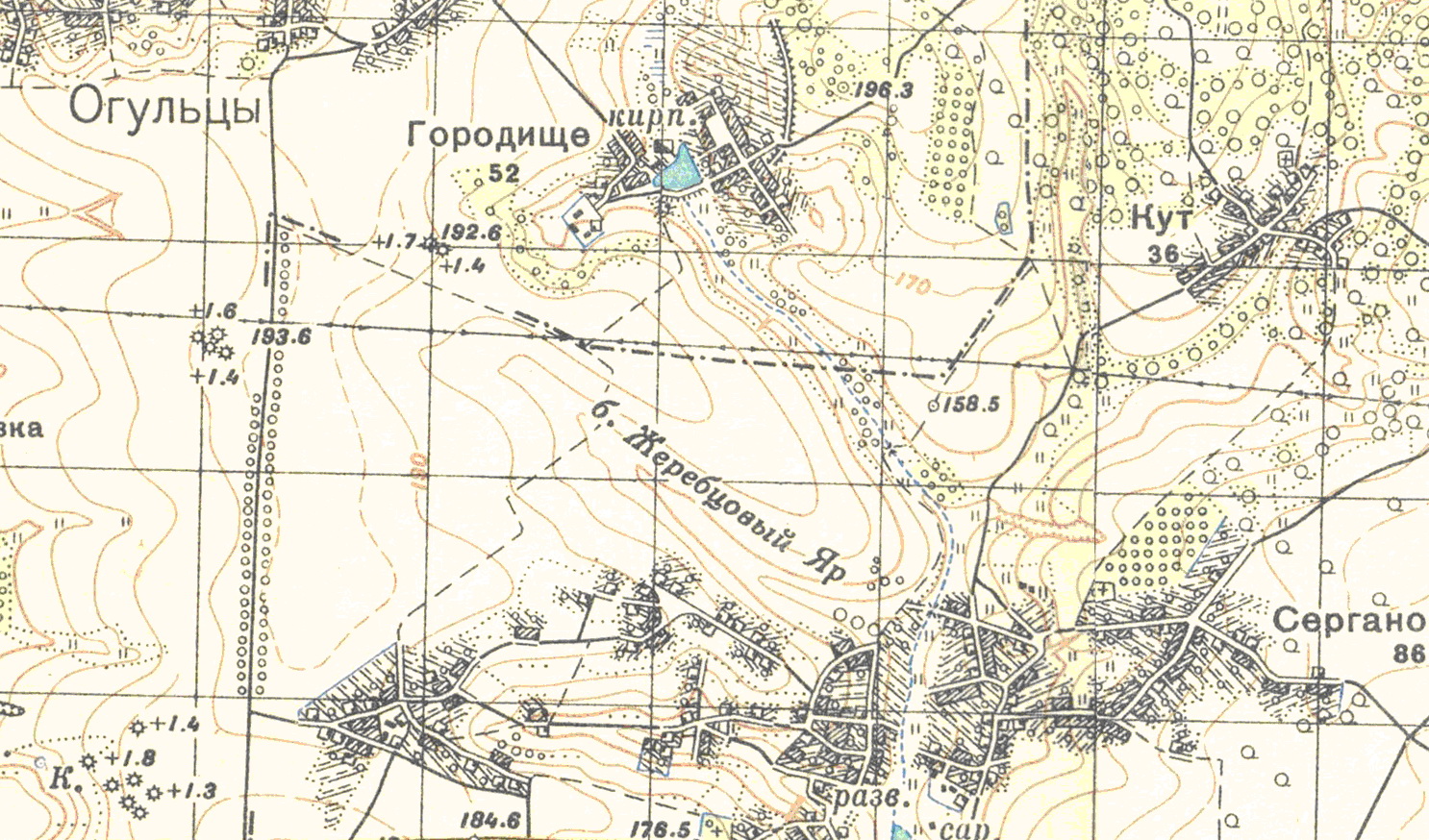
Звідки ми отримуємо інформацію про рельєф? Джерел і способів зараз існує дуже багато. Найбільш буденним є варіант використання фізико-географічних або ж топографічних карт. Зокрема на останніх нерівності земної поверхні репрезентовані горизонталями, інакше – ізогіпсами, тобто кривими, кожна точка яких має однакову висоту над рівнем моря.
Рис.1. Традиційний спосіб представлення рельєфу знайомий нам ще зі шкільних підручників
Багаторічний досвід роботи з такою формою представлення рельєфу сформував потужну методичну базу, яка дозволяє проводити різноманітні морфометричні обрахунки, від найпростіших (вимір крутизни схилу) до складних (складання карт густоти горизонтального розчленування). Зрозуміло, що в наш час високих технологій, традиційне представлення рельєфу поступово замінюється іншими, більш практичними варіантами. Так, думаю всі наші читачі бачили тривимірні комп’ютерні моделі як окремих форм земної поверхні, так і великих її площ.
Такі наочні макети реальних природних об’єктів створюються на основі відповідних цифрових моделей рельєфу (ЦМР). Згідно з Комплексом стандартів Бази топографічних даних, під цифровою моделлю рельєфу розуміють “цифрове подання тривимірних просторових об’єктів (поверхонь, рельєфів) у вигляді тривимірних моделей даних сукупності висотних відміток або відміток глибин та інших значень аплікат у вузлах нерегулярної мережі трикутників або у вузлах регулярної сітки з утворенням матриці висот або як сукупність записів даних про горизонталі (ізогипси, ізобати) або інші ізолінії”.
Говорячи спрощено, ЦМР є комп’ютерною моделлю, яка містить детальну інформацію про значення абсолютної висоти земної поверхні. Для просунутих читачів зауважимо, що в англомовній літературі розрізняють цифрову модель висот (digital elevation model, DEM) і похідну від неї цифрову модель рельєфу (digital terrain model, DTM) як сукупність похідних морфометричних показників (1).
Первинні дані цифрового моделювання рельєфу можуть бути наочно представлені у вигляді двох найбільш поширених способів представлень поверхонь: регулярної мережі висот або ж нерегулярної триангуляційної мережі. Перший спосіб представлення з легкої руки відомого «монстра» ГІС забезпечення фірми ESRI зараз в Україні все частіше називають GRID-моделлю. Другий отримав скорочення TIN (triangulated irregular network – нерегулярна триангуляціна мережа).
GRID-модель має растрову структуру, що утворюється шляхом розбиття простору на однакові неподільні чарунки або ж пікселі (від англійського picture element). Останні зазвичай мають квадратну форму та містять інформацію про висоту земної поверхні над рівнем моря. Як правило саме GRID є основою глобальних та національних моделей висот. Зокрема Геологічна служба США (USGS), в рамках проекту Національна карта (The National Map) пропонує п’ять наборів даних про рельєф у вигляді растрової структури, які відрізняються за технологіями отримання, роздільною здатністю та просторовим охопленням. Також саме GRID-модель лежить у основі вільних глобальних ЦМР – таких як GMTED2010 та ASTER GDEM2.
Структура TIN вичерпно описується самою назвою моделі – нерегулярна триангуляційна мережа. Її основою є набір нерегулярно розташованих точок, які з’єднуються лініями таким чином, щоб утворились трикутники. Отже результатом є багатогранна модель рельєфу місцевості, яка складається з численних трикутників з висотними відмітками висоти у вершинах.
 |
 |
| TIN | GRID |
Рисунок 2. Два способи представлення рельєфу в ЦМР
Кожна з моделей має свої переваги та недоліки. Якщо коротко, то TIN займає в декілька разів менше місця в пам’яті комп’ютера ніж GRID, що обумовлюється її векторною структурою. І саме ж вона обумовлює більші затрати машинного часу на обробку моделі. Також вважається, що TIN краще підходить для відображення рельєфу гірських районів, тоді як GRID більше підходить для презентації рівнинних територій.
А зараз трохи зупинимось на теорії.
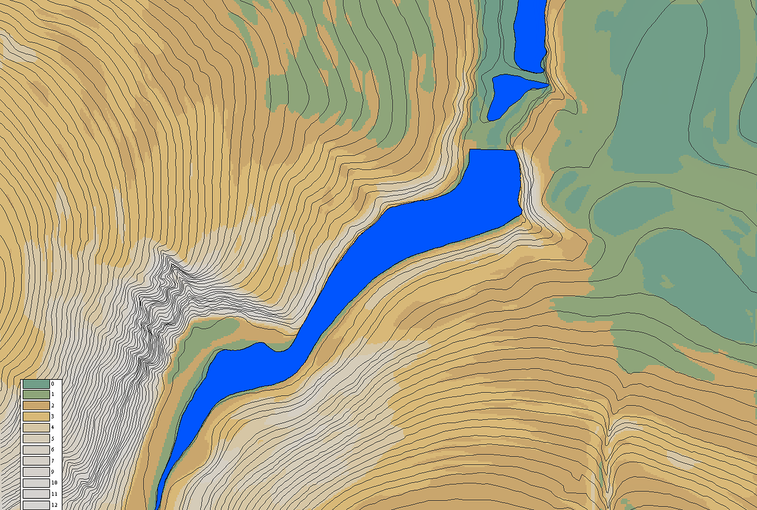
Наприклад, для GRID моделі візуальний аналіз поверхні, яка утворюється в результаті поєднання чарунок зі значеннями висот, нескладний. Здається, навіть старшокласник зможе розібратись з цим зображенням, та виявити на ньому хоча б пагорби та яри. (Принаймні нам хочеться в це вірити:)) Ще простішим буде аналіз за умов тривимірної візуалізації цієї поверхні (рис. 3), тут вже помилок не буде ні в кого.
 |
 |
Рисунок 3. Тривимірна візуалізація цифрової моделі рельєфу
Але ж ця модель, хоча і є дуже красивою, мало що може нам дати в практичному аспекті. Адже серйозні справи вимагають серйозного математичного підходу та відповідних критеріїв оцінювання рельєфу.
До речі, подивитись на реальну місцевість, рельєф якої відображений на рисунку 2, можна віртуально на мапі або ж безпосередньо в польових умовах, проїхавши 13 км від Харкова по Київській трасі до м. Люботин.
Безумовно, найбільш фундаментальними та широко застосовуваними геоморфологічними параметрами є ухил та експозиція нахиленої поверхні, тобто, схилу. Почнемо з ухила, який є показником крутизни схилу та розраховується як перевищення місцевості (a) до горизонтального прокладання (b), на якому воно спостерігається (рис. 4).
Рисунок 4. Ухил схилу
Тобто, величина ухилу дорівнює тангенсу кута α. Говорячи ще більш математично, ухил є першою похідною від висоти, оскільки характеризує інтенсивність зміни її значень в просторі.
Перетворити растрову модель висот на карту ухилів (якщо ви працюєте з GRID), або ж визначити крутизну ребер-трикутників (у випадку TIN) здатна практично будь-яка ГІС. При використанні растрової моделі для визначення крутизни схилу зазвичай використовують відомий алгоритм, що найчастіше пов’язують з роботою Zevenbergen-Thorne (1987).
Розглянемо його основні етапи на прикладі субматриці висот 3 на 3 пікселя (рис.5). Всі розрахунки будемо проводити для визначення крутизни центральної чарунки, яка виділена блакитним кольором. Цифри в чарунках позначають висоту (z), L – відстань між центрами чарунок, інакше – просторова роздільна здатність растру. Жовтим кольором виділені пікселі, значення яких будуть враховані при розрахунках ухилу.
Спочатку обчислюються градієнти зміни висот вздовж двох головних осей х і у:
dz/dx = [ 62 – 61 ] / 2*L
dz/dy = [ 65 – 59 ] / 2*L
Далі для центральної чарунки субматриці обраховується «інтегральний» ухил (slope):
slope = arctg (√ ([dz/dx]2+ [dz/dy]2))
Рисунок 5. Приклад розрахунку ухилу
Після цього залишається запустити даний алгоритм по всьому растру. Результатом буде перерахунок значень висот в кожному пікселі растрової ЦМР на значення ухилів та формування картограми крутизни поверхні (рис.6).
Рисунок 6. Картограма крутизни схилів
Все це добре, але ж яка користь від цієї математики вкупі з геоінформатикою пересічній людині?
Дійсно, треба повертатися до землі. Але зробимо це у наступному пості.
__________________
У цьому пості використана графіка Кріса Коула з Noun Project.