Еталонні дані для оцінки точності класифікації космічного знімка

Раніше на сайті вже був оприлюднений пост про оцінку точності класифікації, присвячений створенню матриці помилок. Але тема на цьому на закінчується, бо в неї є чимало цікавих питань. Коли ми оцінюємо точність результатів автоматизованої класифікації, то треба спочатку вирішити два таких питання:

– який спосіб оцінки обрати?

– де взяти еталонні дані для оцінки?

Зараз поговоримо про друге питання. Розберемо практичні його аспекти на прикладі роботи в програмі ENVI. Але підходи є єдиними для будь-якого програмного забезпечення.

Отже, є чотири підходи (нумерація умовна):

1) використання в якості еталону карти, що охоплює всю територію, яку було дешифровано. Вона може бути створена на основі ручної векторизації космічного знімка, або на основі готових векторних шарів.

2) використання в якості еталону навчальної вибірки, за допомогою якої йшло навчання керованої класифікації;

3) використання в якості еталону карти, що охоплює фрагменти території, яку було дешифровано.

4) Використання в якості еталону точок, в яких на місцевості або під час візуального дешифрування знімку визначають реальний клас.

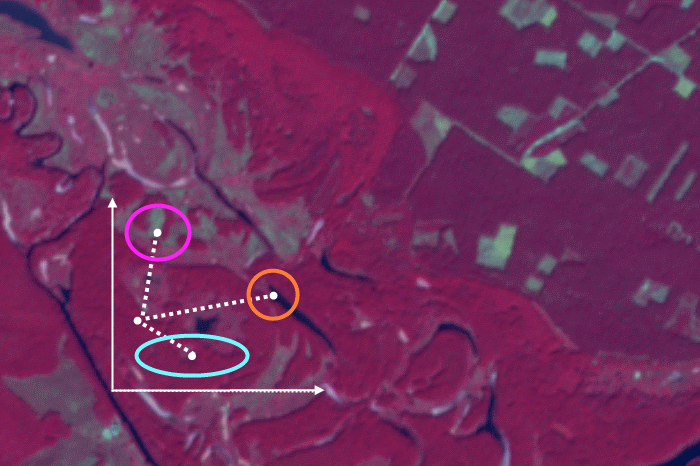
Ці чотири підходи відрізняються за трудомісткістю застосування та правдивістю оцінки. Система цих підходів та їх варіацій зображена на рисунку 1.

Рис. 1. Система підходів до створення еталону класифікації

 

Перший підхід дає найбільш репрезентативний еталон, бо цей еталон охоплює всю територію дешифрування. Такий підхід є зручним коли ми дешифруємо невеликий за площею фрагмент космічного знімка. Але коли треба оцінити якість класифікації великого знімка, такий підхід стає занадто трудомістким. Дуже великим буде об’єм векторизації. Та й ця робота буде безглуздою. Бо якщо ми маємо час щоб уручну відвекторизувати весь знімок, то навіщо нам його взагалі дешифрувати автоматично? Адже в більшості випадків точність ручної векторизації буде більшою, ніж точність автоматичного дешифрування.

Другий, третій та четвертий підходи позбавлені головної вади першого підходу – занадто високої трудомісткості. Це досягається створенням еталону лише для окремих фрагментів досліджуваної території, тобто створення вибірки. Але при цьому стає проблема забезпечення репрезентативності вибірки.

Другий підхід найпростіший і найменш трудомісткій за всі інші. При його застосуванні не треба ніяких додаткових зусиль щоб створити еталон для перевірки точності класифікації. Перед керованою класифікацією завжди створюють навчальну вибірку. І дуже зручно використати її ж в якості еталону для перевірки. Але при цьому не гарантована репрезентативність.

Нам треба оцінити точність для всієї карти класифікації. А за другим підходом ми оцінімо лише точність для фрагментів, що територіально збігаються з навчальною вибіркою. Якщо ці фрагменти є репрезентативними, то з правдивістю оцінки все буде добре. Але не факт, що вони репрезентативні. Користувач створює їх вручну, тому цей процес несе в собі якусь частку суб’єктивності. Окрім того, такий підхід може завищати оцінку точності. Зрозуміло, що там де були пікселі навчальної вибірки, точність буде вище, ніж там де їх не було. Тому цей підхід може мати брак правдивості оцінки.

Третій та четвертий підходи позбавлені суб’єктивності при створенні вибірки для перевірки якості класифікації, бо в їхній основі лежить автоматична генерація вибірки. Ця вибірка може бути випадковою, а може бути систематичною. Систематична вибірка робиться через однакові проміжки. Якщо ми знаємо, що помилки класифікації розподілені у просторі випадково, то можна застосувати для створення еталону систематичну вибірку. Але якщо є імовірність того, що помилки дешифрування розподілені у просторі рівномірно, то краще застосувати випадкову вибірку. Бо при систематичній вибірці у такому разі ми або будемо постійно потрапляти на помилки, або на місця де вони відсутні.

У рамках третього підходу навколо точок вибірки обкреслюють фрагменти території, для якої створюють еталон. Робитися це може за допомогою ручної векторизації знімка. А може робитися на основі наземного обстеження, коли фактичні межі класів картографуються з застосуванням геодезичного обладнання. Чим більше точок у вибірці та чим більше площа фрагментів навколо цих точок, тим репрезентативніше буде еталон. При цьому треба визначати для себе, яку стратегію підвищення репрезентативності та зменшення трудоємності обрати. Робити це можна шляхом підвищення площі фрагментів, а можна шляхом підвищення кількості фрагментів. Звичайно, найбільш оптимальною є компромісна стратегія.

Четвертій підхід – це подальша модифікація третього підходу. В рамках цього підходу площа фрагментів, що обрані для перевірки точності, зменшується до розмірів пікселя. Створення такого еталону найменш трудомістке. Клас до якого мають належати точки еталону можна визначити під час візуального дешифрування космічного знімка. Але в ідеалі треба перевірити фактичний стан цих точок під час польового обстеження. Для цього координати точки завантажують у супутниковий навігатор, знаходять їх на місцевості та встановлюють фактичний клас точок. Чим більше точок вибірки, тим вона буде репрезентативніше, а оцінка точності класифікації буде адекватніше.

В рамках четвертого підходу є два варіанти створення випадкової вибірки. Точки для перевірки можна зробити для всієї площі разом, не звертаючи увагу на межи та площу класів (звичайна вибірка). А можна окремо для кожного класу (стратифікована вибірка). Другий спосіб використають, коли площі класів значно відрізняються.

При стратифікованій вибірці співвідношення кількості точок між класами може строго відповідати пропорції площі класів. Це буде пропорційна стратифікована вибірка. Якщо ця відповідність не виконується, то вибірка буде зватися диспропорційна стратифікована. Її створюють, коли різниця між площами класів дуже велика. В такому разі можна підвищити кількість точок для класів, що мають занадто маленьку площу. А для класів, що мають занадто велику площу, навпаки, зменшити кількість точок. Крайній випадок диспропорційної стратифікованої класифікації, – це коли для всіх класів випадково генерується однакова кількість точок.

 

Проілюструємо те, як відрізняється оцінка точності класифікації при різних підходах до створення еталона. Зробимо це на прикладі з цього посту. Карта класифікації та еталон наведені на рисунку 2. На них є чотири класи: водойми (синій колір), листяні ліси (зеленій колір), хвойні ліси (темно-зелений колір) та інше (сірий колір). Карта класифікації зроблена за допомогою алгоритму паралелепіпеда, еталон – за допомогою ручної векторизації.

Коли ми порівнюємо карту класифікації з еталонною картою для всієї території, то отримаємо загальну точність 94,30%. Будемо вважати, що еталонна карта абсолютно правильна. Якщо це дійсно так, то наведена оцінка загальної точності є найбільш вірною. З нею ми порівнюватимемо оцінки точності за іншими підходами.

Рис. 2. Результат класифікації (ліворуч), та еталон для його перевірки, створеній за першим підходом (праворуч)

 

Тепер подивимося, яку оцінку точності покаже порівняння з еталоном, що був створений за другим підходом. У цьому разі ми маємо вже загальну точність, що дорівнює 99,49%. Ця оцінка є завищеною. Якщо б ми отримали низьке значення точності, то це б було дуже погано. Бо це б значило, що карта класифікації погано відповідає навіть навчальній вибірці. А реальній місцевості вона тим паче буде відповідати ще гірше.

Рис. 3. Еталон, що був створений за другим підходом (ліворуч) та карта класифікації з межами еталонних фрагментів (праворуч, фрагменти для перевірки позначені червоним)

 

Третій та четвертий підходи засновані на використанні випадкової вибірки. Випадковість може лякати. Адже завжди є імовірність випадково створити хибну вибірку та отримати неправильну оцінку точності класифікації. Щоб показати, що це не так жахливо, та як с цим боротися, ми зробили дослід. Для нашої карти класифікації була створена безліч окремих випадкових вибірок. Точніше, 50 вибірок за третім підходом, та 50 вибірок за четвертим підходом.

Для третього підходу в кожної вибірки було 8 круглих фрагментів з радіусом 13 пікселів. Приклад одного з таких еталонів наведений на рисунку 4.

Рис. 4. Еталон, що був створений за третім підходом (ліворуч), та карта класифікації з межами еталонних фрагментів (праворуч, фрагменти для перевірки позначені червоними колами)

 

На рисунку 5 показаний розподіл значень точності, отриманих за третім підходом. Вона змінюється від 90,01 % до 97,92%. Але в середньому вона дорівнює 94,33%, а половина значень знаходиться у діапазоні від 93,82% до 95,13%.

Рис. 5. Гістограма значень точності, отриманих за третім підходом

 

Для четвертого підходу зроблено 50 випадкових стратифікованих вибірок по 100 точок у кожної. Між класами розподіл точок був диспропорційний: водойми – 10 точок, листяні ліси – 20 точок, хвойні ліси – 30 точок, інше – 40 точок (вибірка стратифікована диспропорційна). Приклад одного з таких еталонів наведений на рисунку 6.

Рис.6. Еталон, що був створений за четвертим підходом (ліворуч) та карта класифікації з еталонними точками (праворуч, точки позначені червоним)

 

На рисунку 7 показаний розподіл значень точності, отриманих за четвертим підходом. Вона змінюється від 89,00 до 99,00%. Але в середньому вона дорівнює 93,62%, а половина значень полягає у діапазоні від 92,00 до 95,00%.

Рис. 7. Гістограма значень точності, отриманих за четвертим підходом

 

Тут ми підходимо до наступного питання. Якій підхід краще – третій або четвертий? Щоб дати на нього відповідь, треба порівняти оцінки точність, що дали обидва підходи. На рисунку 8 наведені діаграми розмахів («ящики з вусами») для оцінки точності на основі вибірки точок та вибірки фрагментів. Ми бачимо, обидва підходи у середньому дають приблизно однакову оцінку точності. Вона наближена до реальної точності – 94,3%. Але діапазон можливих значень точності відрізняється. У вибірки точок він ширший. Тобто за третім підходом ми маємо більшу ймовірність, що отримаємо правильну оцінку точності.

Але чому так? Тут все залежить від розміру вибірки. Чим вона більша, тим вище ймовірність отримати правильну оцінку точності. У нашому прикладі за четвертим підходом розмір вибірки 100 точок, а за третім – 4238 точок. І якщо б ми мали не 8, а наприклад 30 фрагментів з такою сумарною площею, оцінка була б ще точніше.

Рис. 8. Діаграми розмахів для оцінок точності, що були отримані за третім та четвертим підходами

 

Щоб проілюструвати, як впливає кількість точок або фрагментів вибірки на точність оцінки, ми зробили ще один дослід. Для нашого прикладу класифікації ми створили випадкові вибірки різного розміру (20, 40, 60, 80, 100, 120 пікселів). Для кожного розміру було створено 50 вибірок. Точки в кожній вибірці були рівномірно розподілені між класами. На основі цих вибірок були отримані оцінки точності класифікації. На рисунку 9 ліворуч ми бачимо, що середнє значення точності класифікації завжди наближено до реального. Але варіювання його різне. Зі зростанням розміру вибірки, воно значно зменшується (рис. 9, праворуч).

Рис. 9. Залежність різниці між отриманою точністю та реальною точністю від розміру вибірки

 

У підсумок цього посту можна сказати наступне. Найбільш ефективним еталоном для перевірки точності класифікації є випадкова вибірка. Чим більше буде її розмір, тим вище ймовірність отримати правильну оцінку точності. На практиці визначення розміру вибірки та її типа (вибірка точок або вибірка фрагментів) – це компроміс між якістю оцінки та трудомісткістю створення вибірки. В ідеалі необхідно ще перевірити належність об’єктів вибірки до класів за допомогою наземного обстеження.